LSTM - Long Short-Term Memory [1997]
Abstract
- RNN의 주요 모델 중 하나로, 장기의존성문제를 해결 가능
- 직전 데이터뿐만 아니라 거시적으로 과거데이터를 고려하여 미래의 데이터를 예측 가능
- RNN은 한 개의 tanh레이어를 가지는 매우 간결한 구조. LSTM은 또한 RNN과 같은 chain 구조를 가지긴 하지만, 단일구조 대신에 매우 특별하게 상호작용하는 4개의 구조를 가진다
- cell-state는 LSTM에서 중요 포인트로 일종의 컨베이어벨트 역할을 한다. 오직 작은 선형 상호작용을 통해 체인 전체에서 작동하며 이는 정보가 쉽게 전달되게 해준다. 덕분에 state가 꽤 오래 경과하더라도 Gradient가 비교적 전파가 잘 된다. LSTM은 이 능력을 없애거나 정보를 cell-state에 추가하는 것이 가능하다
- 각각의 게이트는 정보들이 선택적으로 들어오게 할 수 있는 길이다. 이는 sigmoid 신경망 레이어와 pointwise multiplication operation으로 구성되어있다
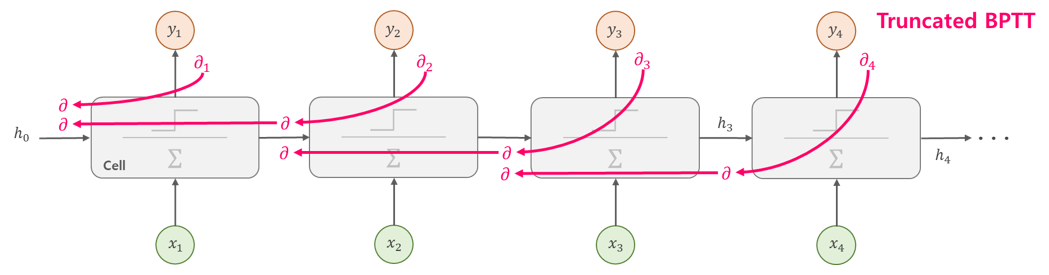
- Backpropagation할 때,
+연산은 distributor역할을 해주기에 gradient를 그대로 전달한다. 때문에 vanishing gradient문제가 생기지 않는다
BPTT를 보완한 Truncated BPTT
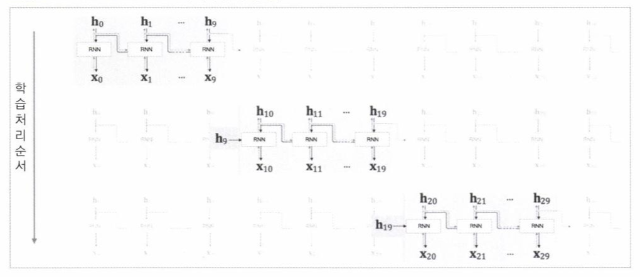
기존 RNN은 매우 비효율적인 메모리를 사용하였습니다. BackProp를 일정단위씩 끊어서 계산하며 일정단위마다 오차를 다시 계산하는 구조입니다. Sequence 데이터를 일정한 크기인 T로 잘라서 배치를 나누듯이 한번에 계산하는 크기를 줄입니다. 한번에 Backpropagation하는 길이가 제한되므로 메모리 사용이 줄어듭니다. 즉, Time-step이 T이상 떨어진 입-출력 관계를 학습되지 않습니다.
Truncated BPTT를 사용할시, 반드시 영향을 주는 데이터 사이의 관계를 침해하지 않게 T로 적절하게 나누었는지, 자신이 학습하고자 하는 것이 어느정도의 시간차이까지 자신이 연관성을 봐야 하는지를 염두해두고 학습을 시켜야합니다. 만약, 연관성이 있는 데이터의 주기가 크고 gradient가 끊기지 않고 연결되어 업데이트가 이루어져야 한다면, 최대한 batch size를 낮추고, 최대한 memory가 큰 GPU를 사용해 긴 길이를 학습해 주는 방법을 사용해야합니다.
길이 T로 쪼개진 Truncation 사이에는 gradient backpropagation이 이루어지지 않습니다. 즉, Time-step이 T이상 떨어진 입-출력 관계는 학습되지 않습니다.
구조
Step 1. Forget Gate : “과거 정보를 버릴지말지 결정하는 과정”
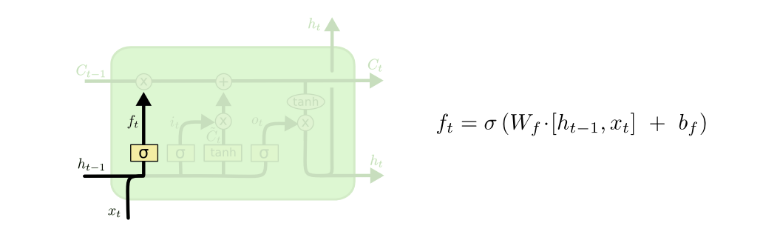
과거의 정보를 통해 맥락을 고려하는것도 중요하지만, 그 정보가 필요하지 않을 경우에는 과감히 버리는 것도 중요합니다. 이전 Input($h_{t-1}$)과 현재 Input($x_t$)을 넣어, cell-state로 가는 과거 정보값이 나옵니다. $h_{t-1}$과 $x_t$를 받아 sigmoid를 취해준 값이 바로 forget gate가 내보내는 값이 됩니다.
Activation Function Sigmoid를 사용했으므로 0또는 1값이 나옵니다.
- 0일 경우, 이전의 cell-state값은 모두 ‘0’이 되어 미래의 결과에 아무런 영향을 주지 않습니다.(Drop)
- 1일 경우, 미래의 예측 결과에 영향을 주도록 이전의 cell-state 값 ($C_{t-1}$)을 그대로 보내 완전히 유지시킵니다.
즉, Forget Gate는 현재 입력과 이전 출력을 고려하여, cell-state의 어떤 값을 버릴지 or 지워버릴지 결정하는 역할을 담당합니다.
Step 2. Input Gate: “현재 정보를 저장(기억)할지 결정하는 과정”
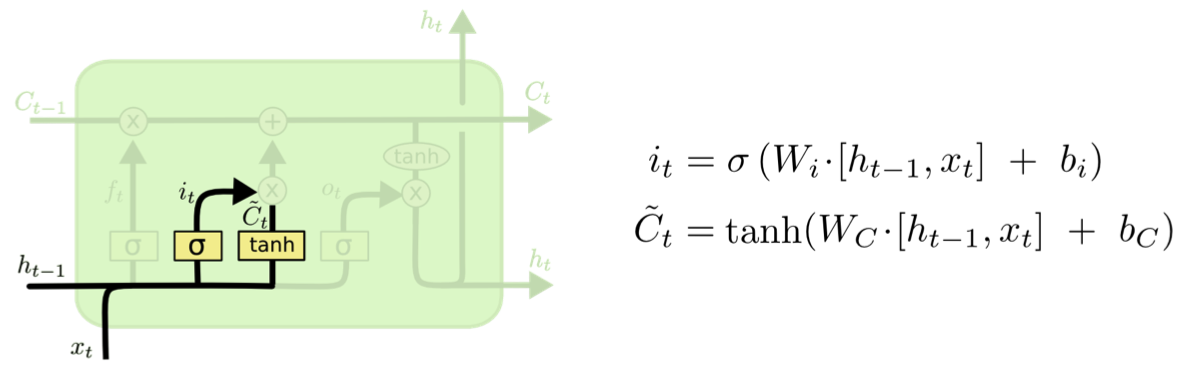
새로운 정보에 대해 cell-state에 저장할지 말지 결정하는 과정이면서 이는 두 가지의 파트로 나뉩니다.
- 'Input gate layer'라고 불리는 sigmoid 레이어는 우리가 업데이트시킬 값에 대해 결정
- tanh 레이어는 $C_t$라는 새로운 vector를 생성하는데, 이는 state에 추가
다음, 이 두가지 정보를 결합해 state에 업데이트 시킵니다. 현재의 cell-state값에 얼마나 더할지 말지를 정하는 역할입니다. (tanh값은 -1, 1의 값을 나타냅니다)
Forget gate의 값과 같은 입력으로 하이퍼볼릭탄젠트를 취해준 다음 연산한 값이 바로 Input gate의 output값이 됩니다.
$i_t$는 시그모이드 함수를 취했기 때문에 범위는 0 ~ 1
$C_t$는 하이퍼볼릭탄젠트 함수를 취했기 때문에 범위는 -1 ~ 1
Step1(Forget gate)과 Step2(Input gate)의 역할은 이전 cell-state 값을 얼마나 버릴지, 지금 입력과 이전 출력으로 얻어진 값을 얼마나 cell-state에 반영할지 정하는 역할
Step 3. Cell state (Update) : “과거 cell-state($C_{t-1}$)를 새로운 state($C_t$)로 업데이트 하는 과정”
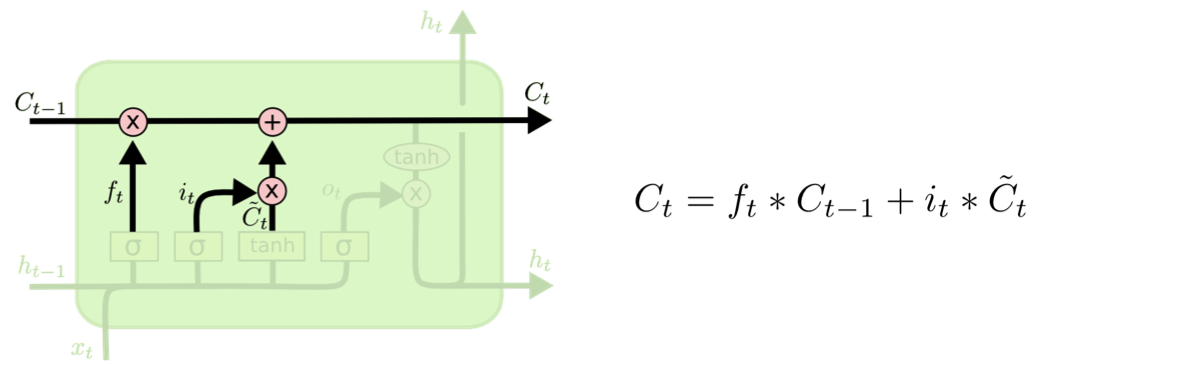
예전 cell-state인 $C_{t-1}$를 업데이트시켜 새로운 cell-state인 $C_t$로 만들어주는 과정입니다. 이 전의 과정에서 값들을 모두 지정시켜놨으므로 적용만 시켜주면됩니다.
이전 step에서 결정한 것들을 잊어버리고 예전 state인 $C_{t-1}$와 $f_t$를 곱하여, $i_t * C_t$를 더해줍니다. 이를 통해, 새로운 값이 나왔을 것이고, 이는 각각의 state에 업데이트 될 것입니다.
해당 스텝은 예전 정보를 잊어버리고 이전 스텝에서 결정했던 정보들을 추가해주는 과정이라고 생각하면 됩니다.
“Update, scaled by now much we decide to update”
Step 4. Output Gate (hidden state) : “어떤 출력값을 출력할지 결정하는 과정”
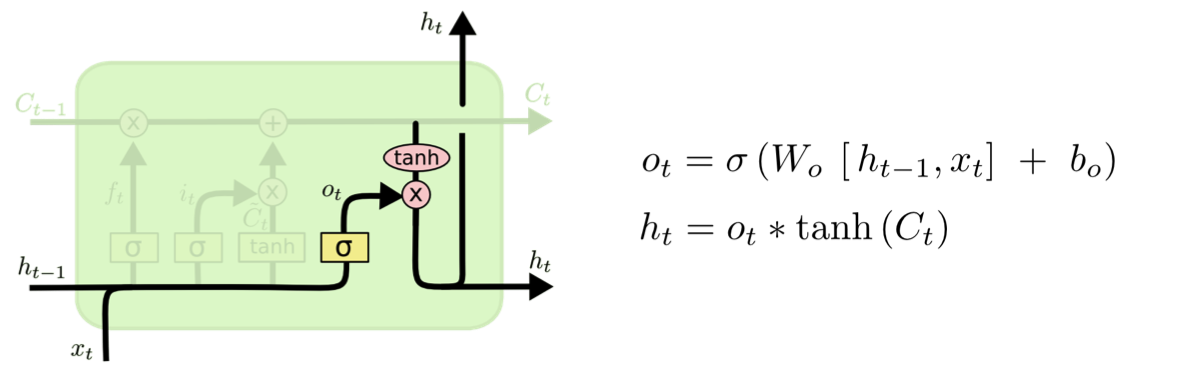
output값은 우리의 cell-state에 기반한 정보들이 될 것이나, Filter를 적용한 후의 값이 될것입니다.
- sigmoid 함수를 적용한 Output 값 도출
- 전 과정의 hidden state를 지나쳐온 $C_t$값을 tanh함수에 통과 후 output값 도출
- 위 1번의 $o_t$와 2번의 $tanh(C_t)$를 곱함
최종적으로 얻어진 cell-state값을 얼마나 빼낼지 결정하는 역할
LSTM에 ReLU함수가 잘 어울릴 수 있다??
ReLU함수는 매우 간단한 구조로 0보다 값이 크면 Input값을 직접 리턴시켜줍니다. 이를 통해 네트워크는 선형함수로 더 근접하는 값을 가능하게해줍니다.
하이퍼볼릭탄젠트 함수보단 ReLU함수를 더 많이 사용하는 추세로, 많은 레이어에서 vanishing gradient problem문제를 일으키므로 사용되지 않고 있습니다. ReLU함수는 더 높은 성능과 더 빠른 학습을 통해 해당 문제를 억제시켜줍니다.
또한 GPU 환경에서 더 깊은 신경망을 구성하는것과 같이 하드웨어의 가용성이 상승하면서 학습이 어렵게 되기 때문에 sigmoid와 tanh를 굳이 사용하지 않는다고 합니다.
- 매우 간단한 연산방법
- sigmoid나 tanh와 달리 매우 간단한 연산을 통해 값을 리턴
- 추가적인 계산이 필요없음
- Representational Sparsity
- sigmoid나 tanh와 달리 output을 0이나 0의 근사치로 리턴
- 이는 layer를 쌓는 신경망 구조에서 상당히 중요한데, 학습 속도나 모델을 간단화시키는데에 매우 중요한 개념
- Linear Behavior
- Linear 함수처럼 사용 가능
- 일반적으로 신경망 구조에서 Linear함수를 사용하면 매우 간단하게 최적화 가능
- 그러므로, ReLU함수를 사용하면 vanishing gradient problem을 피할 수 있음
- Train more deeper network
- 사전학습없이 깊은 다층퍼셉트론 네트워크를 비선형함수로 activate해 성공적으로 학습시킬 수 있음
데이터와 분석요건에 따라 많은 변수들이 생길테지만, ReLU함수는 굉장한 output에 도달할 수 있으며 전통적으로 LSTM에 사용되어지고있는 함수입니다. 다음은 시계열 데이터로 모든 column은 양수값인 데이터이며 주 변동성을 예측하려는 hotel cancellation 데이터를 LSTM으로 돌린 값이라고 합니다.

RMSE 값은 약 4point 차이, MFE값은 현저하게 낮게 측정되었습니다. sigmoid함수는 트렌드 값을 잡아내려고하며, 경향성 면에선 ReLU함수가 더 우월하다고 할 수 있겠습니다.
다양한 LSTM 모델
1. Peephole Connection
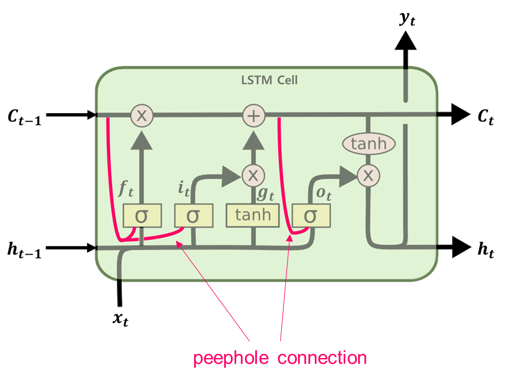
Peephole Connection 모델은 게이트가 cell-state 자체를 입력값으로 받는 방식을 의미합니다.
- LSTM이 가지는 한계
- Input과 Output의 모든 셀로부터 각각의 gate는 연결을 받지만 여기엔 방향이 없다
- 이 모든 것들을 직접적으로 cell output에서 발견되며 거의 0에 값에 가까운 값을 가진다
- 이 필수적인 정보의 결핍현상은 성능에 있어서 안 좋은 영향을 미친다
이에 Peeophole Connection은 가중합된 “Peephole” 연결을 같은 메모리 block의 gate에 더해주어 한계점을 해소시켜줍니다.
일반적인 LSTM에서는 gate controller는 입력 $x_t$와 이전 단기상태인 $h_{t-1}$만을 고려합니다. 이들에게 장기상태 $c_t$의 정보도 노출시켜 더 많은 문맥을 감지하게 하는것입니다.
- $c_{t-1}$ 가 forget gate와 input gate의 제어기 $f_t$와 $i_t$에 입력으로 추가된다
- $c_t$가 출력게이트의 제어기 $o_t$의 입력으로 추가된다
2. Couple with Forget gate and Input gate
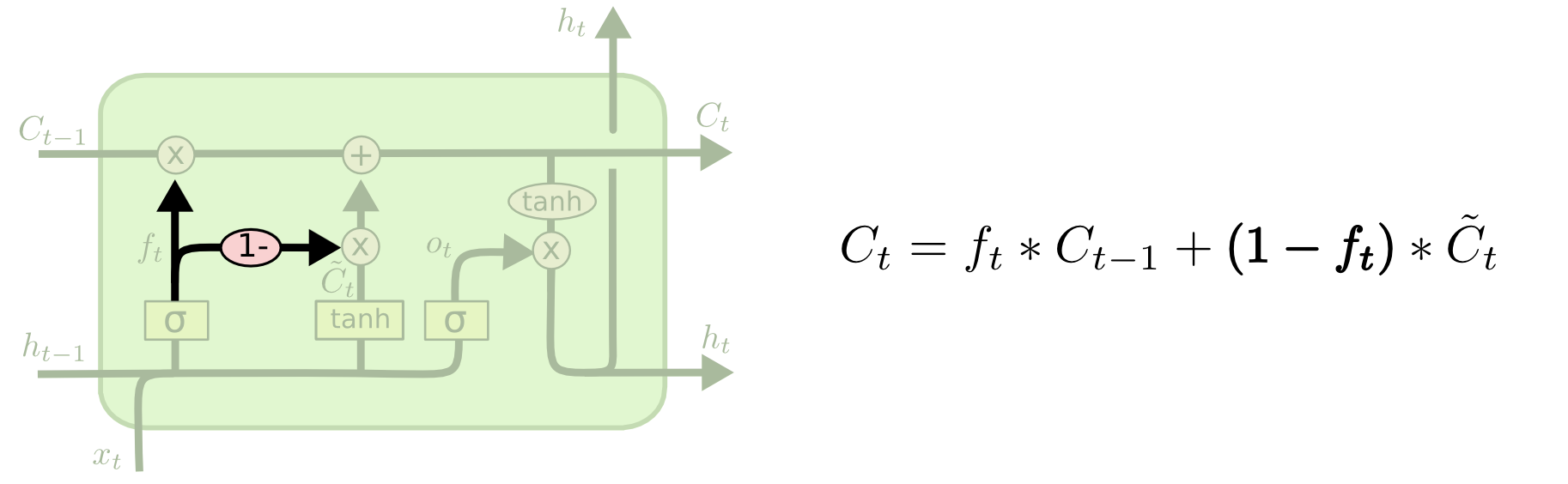
Forget gate와 Input gate, 두 개의 과정을 따로따로 수행하는 것이 아니라, 이를 동시에 결정하는 방식입니다. 이때 새로운 값이 제공될 때만 이전값을 drop하게 됩니다.
3. Gated Recurrent Unit (GRU)
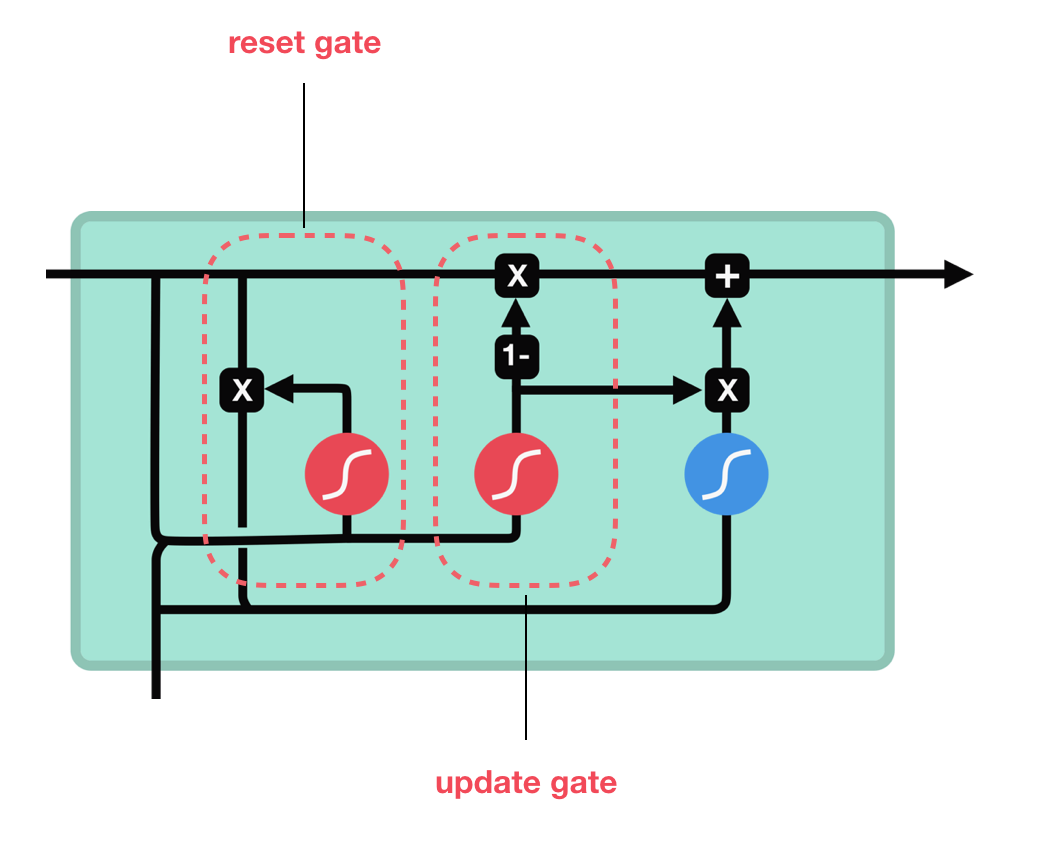
GRU는 LSTM과 비슷한 구조를 가지며 RNN의 새로운 generation 입니다. GRU는 cell-state를 제거했으며 정보들을 전이하기위해 hidden state를 사용합니다
GRU는 기존 LSTM과 꽤나 다른 버젼으로 forget gate와 input gate를 하나의 Update Gate로 통일하였습니다.
Update Gate
Update gate는 LSTM의 forget gate, input gate와 유사하게 동작합니다. 정보를 버릴지 추가할지 결정하는 역할을 수행합니다.
Reset Gate
Reset gate는 과거 정보를 얼마나 잊어버릴지 결정하는 또다른 게이트입니다.
이게 GRU에 대한 내용이며, GRU는 더 낮은 tensor에서 동작합니다. 그러므로 LSTM보다 좀 더 빠른 모델이라고 할 수 있겠습니다. 그러나, 어느 모델이 확실한 승자일 순 없을것입니다. 그렇기에 연구진들은 어떤 task에 어떤 model이 적합할지 씨름해야할 것입니다.
GRU에 대해선 추후에 더 자세하게 따로 포스팅 할 예정입니다.