RNN | LEE

Abstract

기존의 Neural Network는 맥락이 전혀 고려되지 않은 단순한 구조였습니다. 이에 Hidden Layer를 도입하여 Speech Recognition, Language Modeling, Machine Translation, Image Captioning, etc.. 많은 문제를 해결했습니다.

RNN은 Hidden Node에서 Activation Function을 통해 나온 결과값을 출력층 방향으로도 보내면서 동시에 다시 Hidden Node의 다음 계산의 입력으로 보내는 특징을 가집니다.

$x_t$ 는 입력층의 Input Vector, $y_t$는 출력층의 출력 벡터

RNN 에서는 hidden layer에서 활성화함수를 통해 결과를 내보내는 역할을 하는 노드를 셀(Cell)이라고 합니다. 이 셀은 이전의 값을 기억하려고하는 일종의 메모리역할을 수행하므로 이를 Memory-Cell 또는 RNN-Cell 이라고 표현합니다.

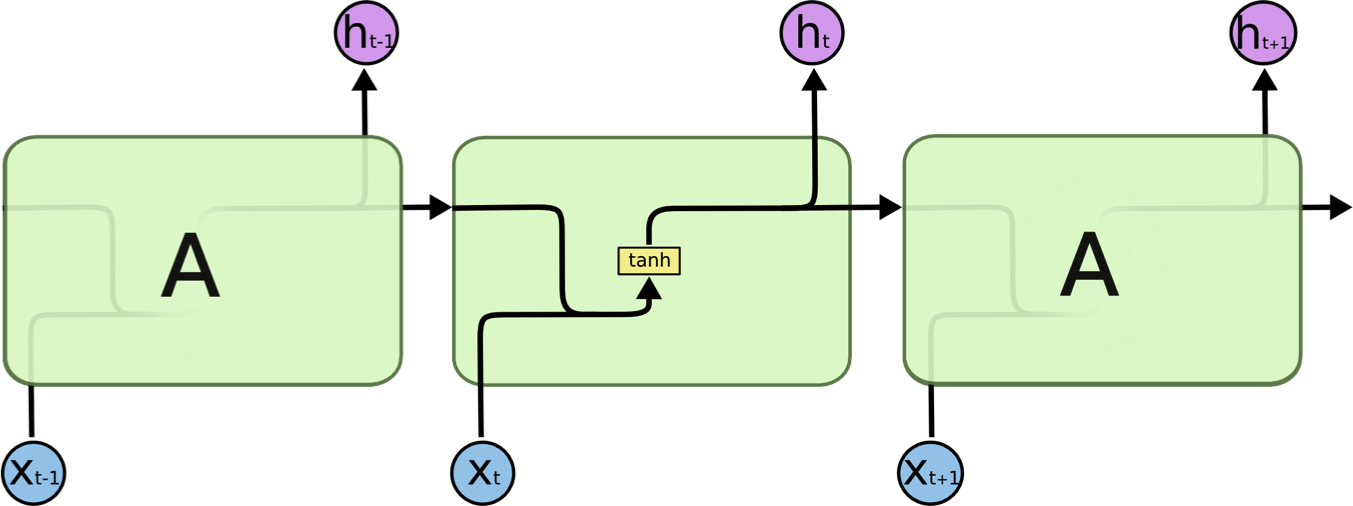
Hidden layer의 메모리셀은 각각의 시점(Time-step)에서 바로 이전 시점에서의 은닉층의 메모리 셀에서 나온 값을 자신의 입력으로 사용하는 재귀적(Recursive)활동을 하고 있습니다. 즉, 현재 시점 $t$ 에서의 메모리셀이 갖고있는 과거의 메모리 셀들의 값에 영향을 받은 것입니다.

여기서 메모리셀이 갖고 있는 이 값을 은닉 상태(Hidden State) 라고 합니다.

hidden state는 메모리셀 출력층방향으로 또는 다음 시점인 $t+1$의 자신에게 보내는 값. 즉, $t$ 시점의 메모리셀은 $t-1$ 시점의 메모리셀이 보낸 은닉상태값을 $t$ 시점의 은닉상태 계산을 위한 입력으로 사용됩니다.

직전 데이터($t-1$)와 현재 데이터($t$)간의 상관관계를 고려해 다음의 데이터($t+1$)를 예측하고자, 과거의 데이터도 반영한 신경망 모델을 만든 것입니다.

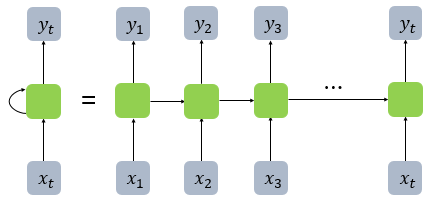
Feed Forward Neural Network에서는 뉴런이란 단위롤 사용했지만, RNN에서는 뉴런이란 단위보다는 입력층과 출력층에서는 입력벡터와 출력벡터, 은닉층에서는 은닉상태라는 표현을 주로 사용합니다.

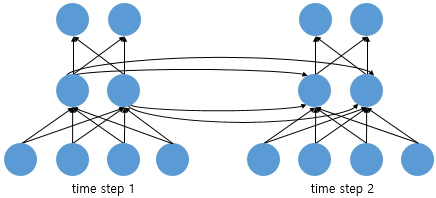
위 그림은 RNN을 뉴런단위로 시각화한 이미지입니다.

input_dim = 4, hidden_state = 2, output_dim = 2, time_step = 2의 값을 가지며 RNN에선 2~3개의 layer를 쌓는 것이 일반적입니다.

구조

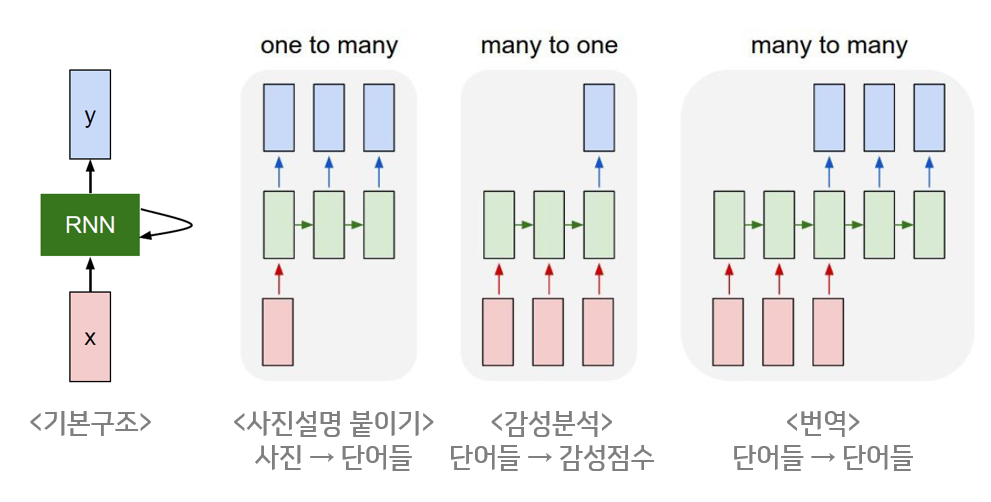
위와 같이, RNN은 입력벡터(입력)와 출력벡터(출력)의 길이를 다르게 설계할 수 있으므로, 다양한 용도로 사용할 수 있습니다. 위의 그림은 입력과 출력의 길이에 따라서 달라지는 RNN을 다양한 형태로 보여줍니다. 시퀀스의 길이와 관계없이 Input과 Output을 받아들일 수 있는 네트워크 구조이기 때문에 필요에 따라 다양하고 유연하게 구조를 만들 수 있다는 점이 RNN의 가장 큰 장점입니다.

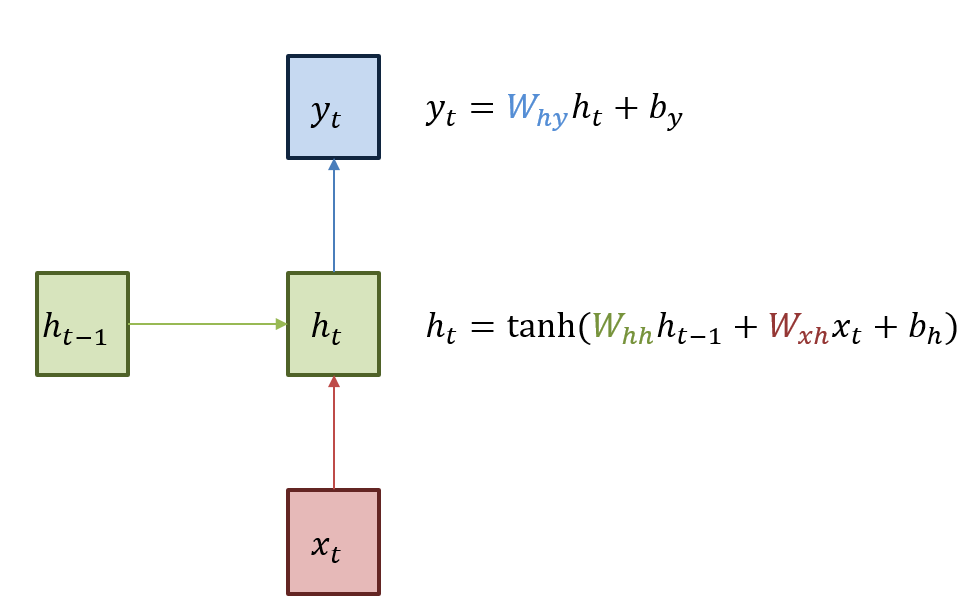
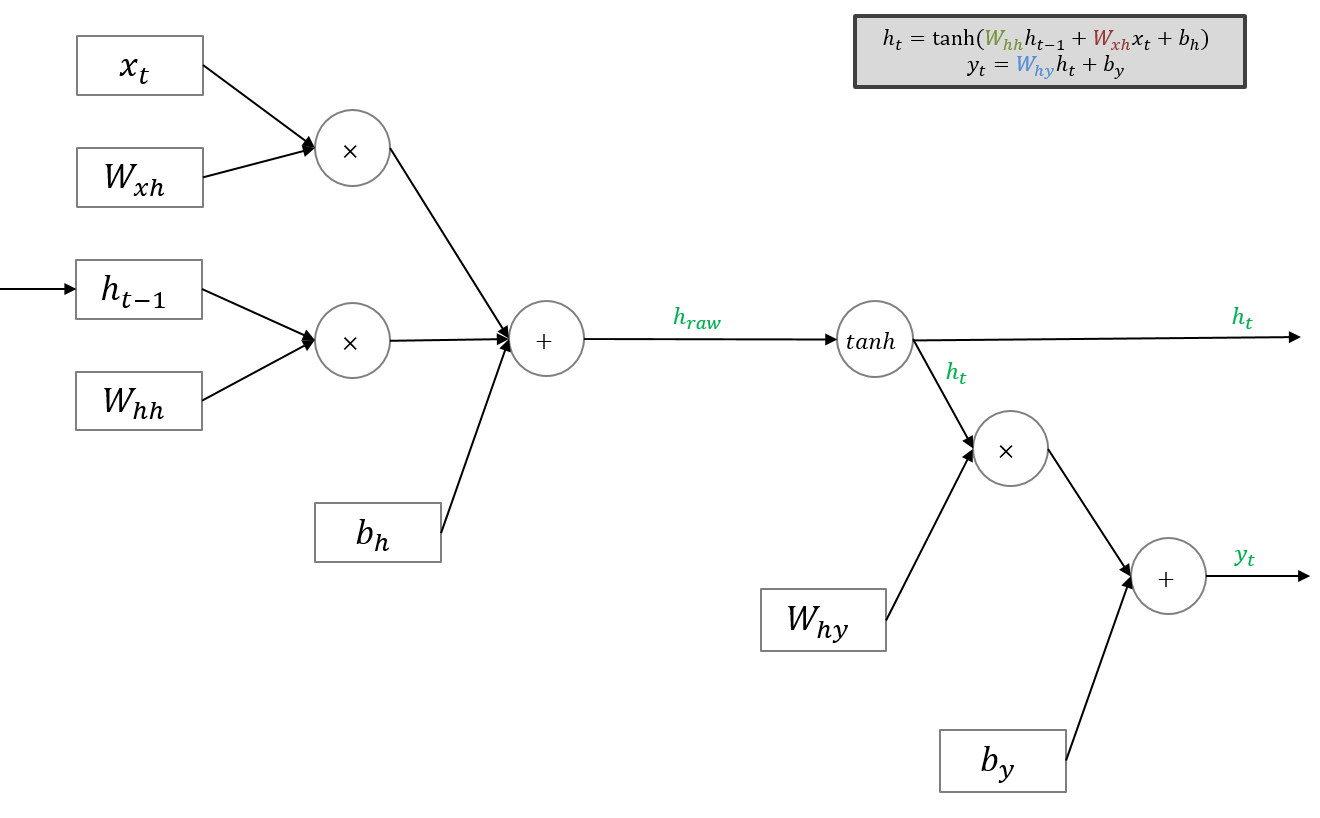
현재 상태의 hidden state $h_t$는 직전 시점의 hidden state $h_{t-1}$를 받아 갱신됩니다.

Output $y_t$는 $h_t$를 전달받아 갱신되는 구조이며 hidden state의 활성함수는 비선형함수인 하이퍼볼릭탄젠트를 사용합니다.

RNN이 학습하는 Parameter값은 다음과 같습니다.

입력층(input x)를 hidden layer $h$로 보내는 $W_{xh}$
이전 hidden layer $h$에서 다음 hidden layer $h$로 보내는 $W_{hh}$
hidden layer $h$에서 Output $y$로 보내는 $W_{hy}$

이 값들은 모든 시점에서 값을 동일하게 공유(shared weights)합니다. 만약 은닉층이 2개 이상일 경우에는 은닉층 2개의 가중치는 서로 다르게 될 것입니다.

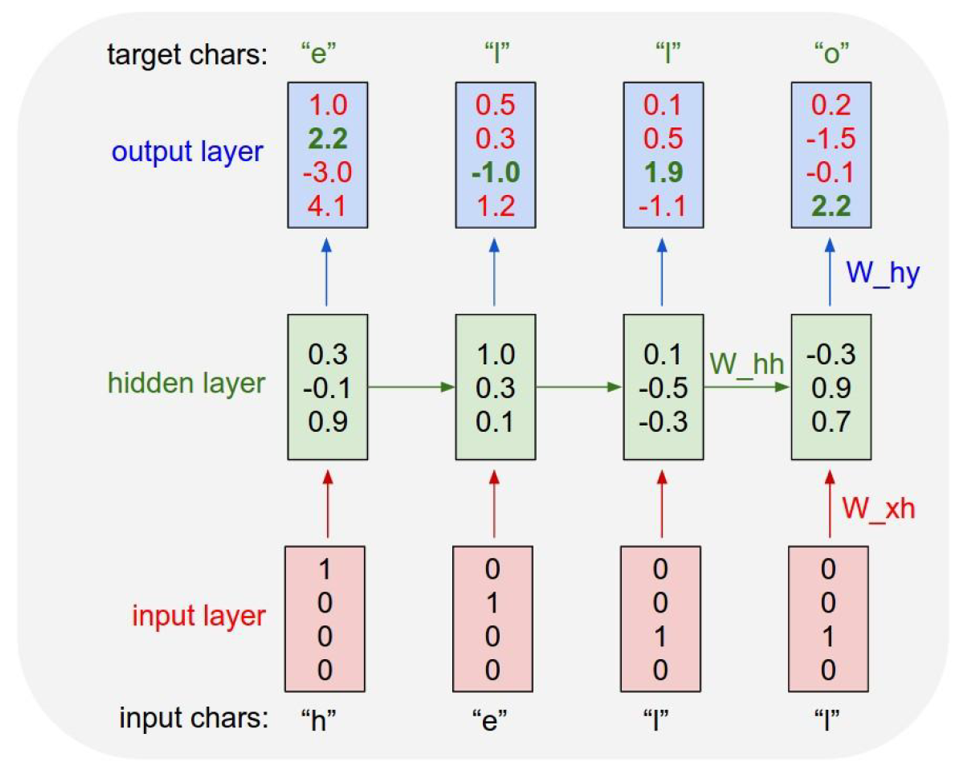
학습데이터의 글자는 h, e, l, o 로 4개입니다. 이를 one-hot vector 거치면 [1, 0, 0, 0], [0, 1 ,0, 0], [0, 0, 1, 0], [0, 0, 0, 1] 의 결과값을 가질것입니다.

$x1$은 [1, 0, 0, 0] > $h_1$ [0.3, -0.1, 0.9] 생성 > $y_1$ [1.0, 2.2, -3.0, 4.1] 생성할 것입니다. 두번째, 세번째, 네번째 단계들도 모두 갱신하게 될 것이며, 이 과정을 순전파(Foward Propagation)라고 칭합니다.

RNN도 정답을 필요로 하는데, 모델엘 정답을 알려줘야 모델이 parameter를 적절히 갱신해 나갈 것입니다. 이 경우엔 바로 다음 글자가 정답이 될 것입니다. 예를 들어, h의 다음 정답은 e, 그 다음 정답은 l, 그 다음 정답은 l, 그 다음은 e가 될 것입니다.

$y_1$에 진한 녹색으로 표시된 숫자가 있는데 정답에 해당하는 인덱스를 의미합니다. 이 정보를 바탕으로 역전파(Backpropagation)를 수행해 parameter값들을 갱신해 나갑니다. 이와 같이 다른 신경망과 마찬가지로 RNN 역시 경사 하강법(Gradient Descent)과 오차역전파를 이용해 학습합니다. 정확하게는 시간의 흐름에 따라 작업을 하기때문에 역전파를 확장한 BPTT(Back-Propagation Through Time)를 사용해 학습합니다.

BPTT

BPTT는 필연적으로 gradient가 발산(Exploding), 소실(Vanishing)문제가 발생합니다. 에러(학습해야하는 분량)가 이전의 시간으로 전달될수록 점차 희석될 것입니다. 에러가 학습 파라미터(weight, bias)에 잘 전달되지 않으면, 모델링이 제대로 이루어질 수 없습니다. 반대로 필요하지 않은 이전 정보들까지도 학습하게되어 예측이 잘 되지 않을 수 있습니다.

Truncated BPTT

장기기억을 적절한 단위로 쪼개서 학습시키자는 것이 아이디어이며, 이는 앞서 기술했던 vanishing and exploding problem을 해결하면서, 동시에 특정 input에 적합한 시간 window를 사용하자는 것입니다.

Truncated BPTT에선 BPTT를 얼마나 시간적으로 긴 단위에 걸쳐서 할 것이지(=window_size), 그리고 얼마나 촘촘하게 할 것인지(=shifting_size)를 설정할 수 있습니다.

RNN의 순전파 / 역전파

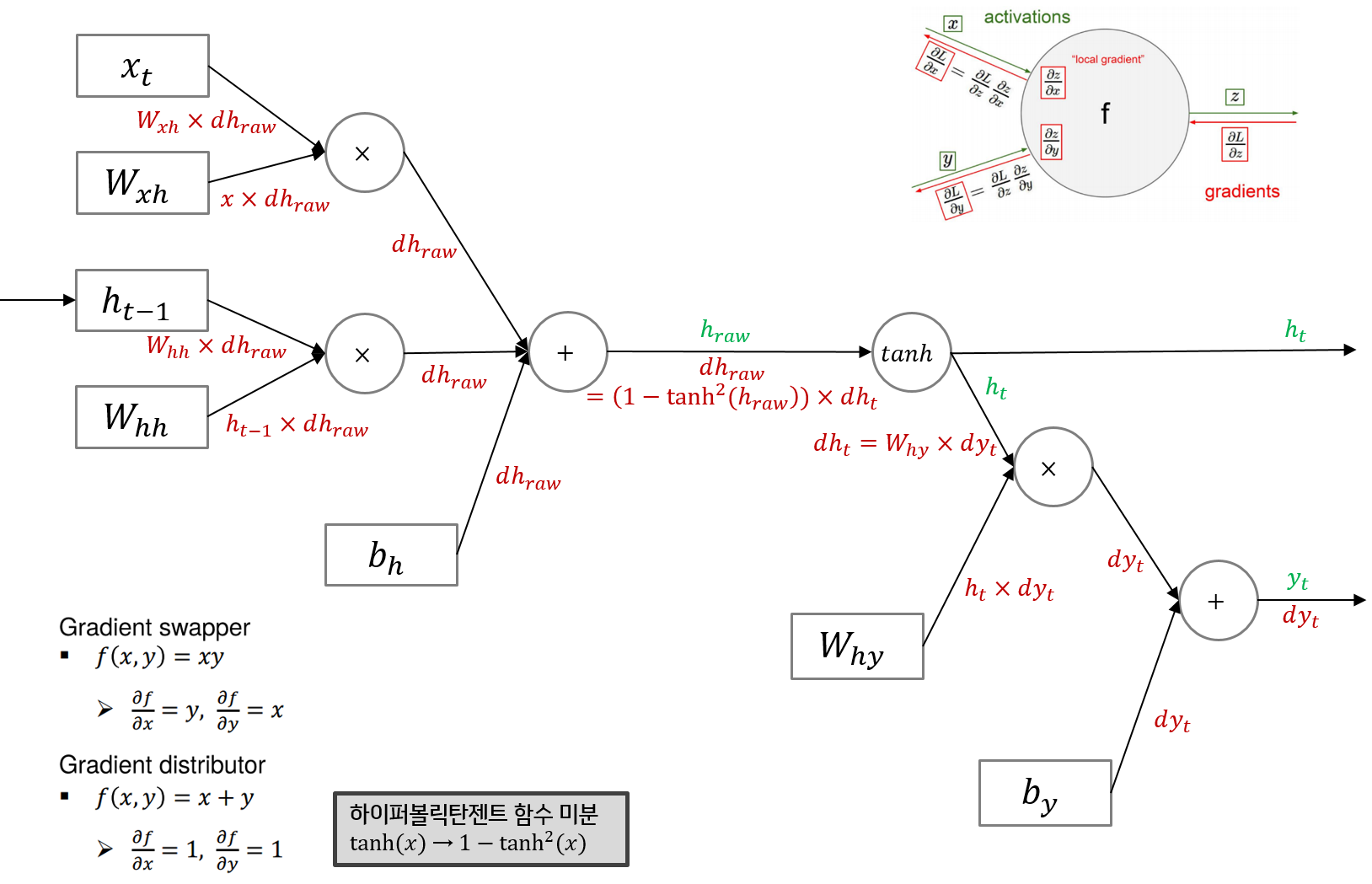
여기서 RNN의 단점이 드러나는데, RNN은 관련 정보와 그 정보를 사용하는 지점 사이 거리가 멀 경우 역전파시 gradient가 점차 줄어 학습 능력이 크게 저하되는 것으로 알려져있습니다. 이를 Vanishing Gradient Problem이라고 합니다.

Activation Function

ReLU함수를 사용하지 않는 이유

필자는 기존 딥러닝 프레임워크에서 자주 사용되는 활성화함수인 ReLU함수를 왜 사용하지 않을까라는 의문이 들었고 조사해봤습니다.

Quora에 필자와 비슷한 의문점을 제기하는 사람들을 찾아 볼 수 있었습니다.

Neural Network에서 ReLU는 common하게 사용되는 함수이나 RNN에선 그렇지 못하게 될것이다

ReLU함수는 Gradient-based learning algorithm에선 만족할 만한 성능을 뽑아내지 못 할 것

RNN은 매우 큰 output을 가지고 있기에 ReLU함수는 부적절해보인다. 그래서 값이 튀는 현상이 나타날것으로 예상된다

RNN은 Time Sequential하게 과거의 데이터를 지속적으로 꺼내서 씁니다. 즉, 과거의 값들이 끊임없이 재귀적으로 사용되기 때문에 $(-1, 1)$ 사이의 값으로 Normalization이 반드시 필요합니다. 여기서 ReLU함수를 사용하게되면 0 이상의 값에선 input 값을 그대로 가져가게 되고 time-step이 쌓일수록 발산할 확률이 높아지게됩니다. 그렇기에, output의 값을 Normalization 해줄 수 있는 함수인 sigmoid, tanh가 주로 사용됩니다. Vanishing Gradient 문제를 잡기 위해 사용했던 ReLU는 RNN에선 LSTM 및 tanh로 해결했으므로, 굳이 발산할 가능성이 있는 ReLU를 쓸 필요가 없고, 쓰면 발산합니다.

ReLU함수의 식은 매우 간단한데 반해, Tanh와 Sigmoid함수는 복잡한 삼각법에의한 함수이며 다중곱셈을 시행합니다. 단기의 딥러닝에선 output과 input간의 근사한 관계를 찾아야합니다. 그러나, ReLU는 이러한 결과를 내는데 충분히 복잡하지 않은 함수라고 합니다. 또한 임의의 방식에 따라 값이 발산되는 경향이 있고, 선형 unit을 강하게 규제시키는 경향이 존재합니다. 따라서 RNN모델에선 좀 더 복잡한 공식을 가지면서 -1에서 1의 범위를 가지는 함수인 Tanh를 채택하는 것입니다.

Tanh는 중간값을 다루는 관점에서 더 괜찮은 값들을 도표화하는데 적합한 함수라 할 수 있습니다. 이는 재귀역학적 관점에서 매우 중요한 표인트인데, Monte Carlo Convergence에서 보이듯이, 분수함수(sigmoid)는 천천히 점진적으로 값이 갱신되며 True value값으로 점차 향하게 될 것입니다. Tanh는 0 주변의 균형잡힌 값이 있는데, ReLU는 그렇지 못합니다. 즉, ReLU함수를 취하게 되면, 음수값의 weight는 0으로 리턴되는 것을 의미합니다. ReLU함수는 빠르게 음수값을 0으로 만들려는 경향이 있고, 이를 Deep Network에선 Dead ReLU Problem 이라고 합니다. 이 문제는 RNN에서 gradient 값을 점점 더 낮추는 문제(vanishing gradient problem)를 야기할 뿐만 아니라 이전의 time-step으로부터 전해 들어온 gradient값을 취할 것입니다. 필연적으로, RNN은 기존의 feed-forward network보다 몇몇 시간을 거쳐 더 깊게 들어가야하고 이 과정에서 ReLU 뉴런은 빠르게 죽어나갈것이며 전체 뉴런이 동작하지 않게 될 수 있습니다.

다양한 RNN 모델

IRNN

IRNN paper 『A SimpleWay to Initialize Recurrent Networks of Rectified Linear Units』은 ReLU함수를 사용함으로써 tanh를 사용하면 나타날 수 있는 vanishing and exploding gradient problem에 대한 해결책을 제시하였습니다.

기존 RNN모델은 BPTT를 사용함으로써 에러 미분을 계산하는 과정에서 어려움이 나타났었고 gradient 문제는 장기의존적인 학습에 무리가 많았습니다. 그러면서 이 문제를 해결하기 위해 LSTM으로의 변화가 나타났습니다.

첫번째, 비선형함수인 ReLU함수 사용

두번째, 은닉레이어 기울기값인 $W_{hh}$(Weight Matrix)를 단위행렬로 초기화해주고 bias를 0으로 세팅

현재의 은닉벡터는 이전의 은닉벡터 값을 단순하게 취하게 한 후에 현재의 input에 추가해주고, 모든 음수값은 0으로 치환됩니다. 이러한 input의 부재속에, ReLU함수를 활성화하고 단위행렬을 초기값으로 지정해줍니다. 이를통해, 근본적으로 RNN이 가지는 long-term dependency의 문제를 극복할 수 있을 것이며, LSTM이 가지는 forget-gate의 작동 메커니즘과 비슷한 원리를 가지는 구조를 만들 수 있을것입니다.

이러한 일련의 과정을 해당 논문에선 IRNN이라고 칭하였고, 이는 상당한 성능을 뽑아낸다고 주장했습니다. 또한 더 적은 장기의존성을 가지는 경우, 적은 스칼라값으로 조정된 단위행렬은 더 효율적으로 작동한다는 사실도 밝혔습니다. 이러한 메커니즘은 LSTM의 forget-gate가 메모리를 좀 더 빠르게 손실하기위한 방법과 같은 이치임을 밝혔습니다. 더불어 LSTM과 비교하여 비교적 적은 튜닝, 그리고 더 단순한 메커니즘을 통해 더 좋은 성능을 뽑아낸다는것을 주장했습니다.

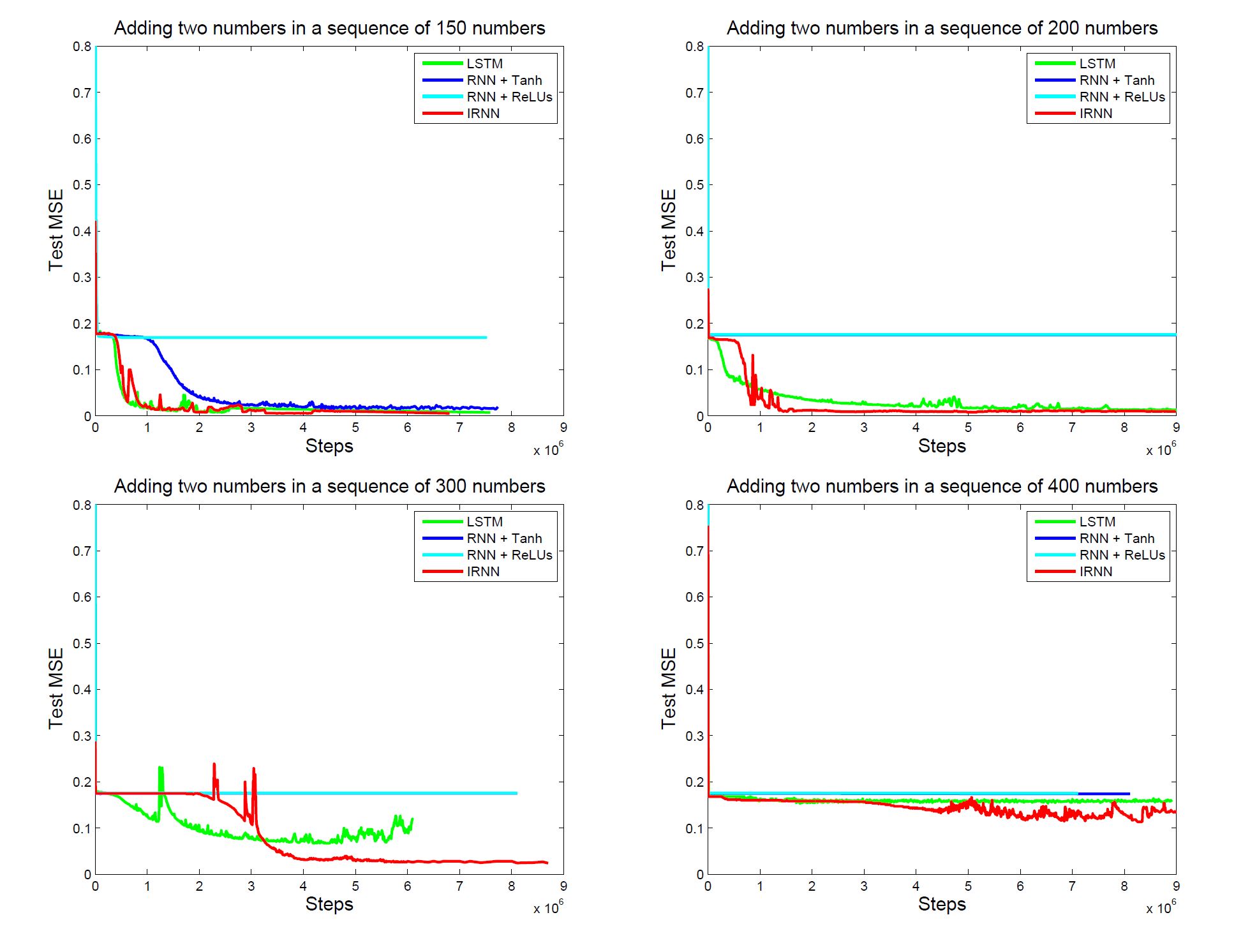
Experiment

LSTM (Setting to a higher initial forget gate bias for long-term dependency)
RNN (tanh)
RNN (ReLU + Gaussian Initialization)
IRNN

IRNN성과

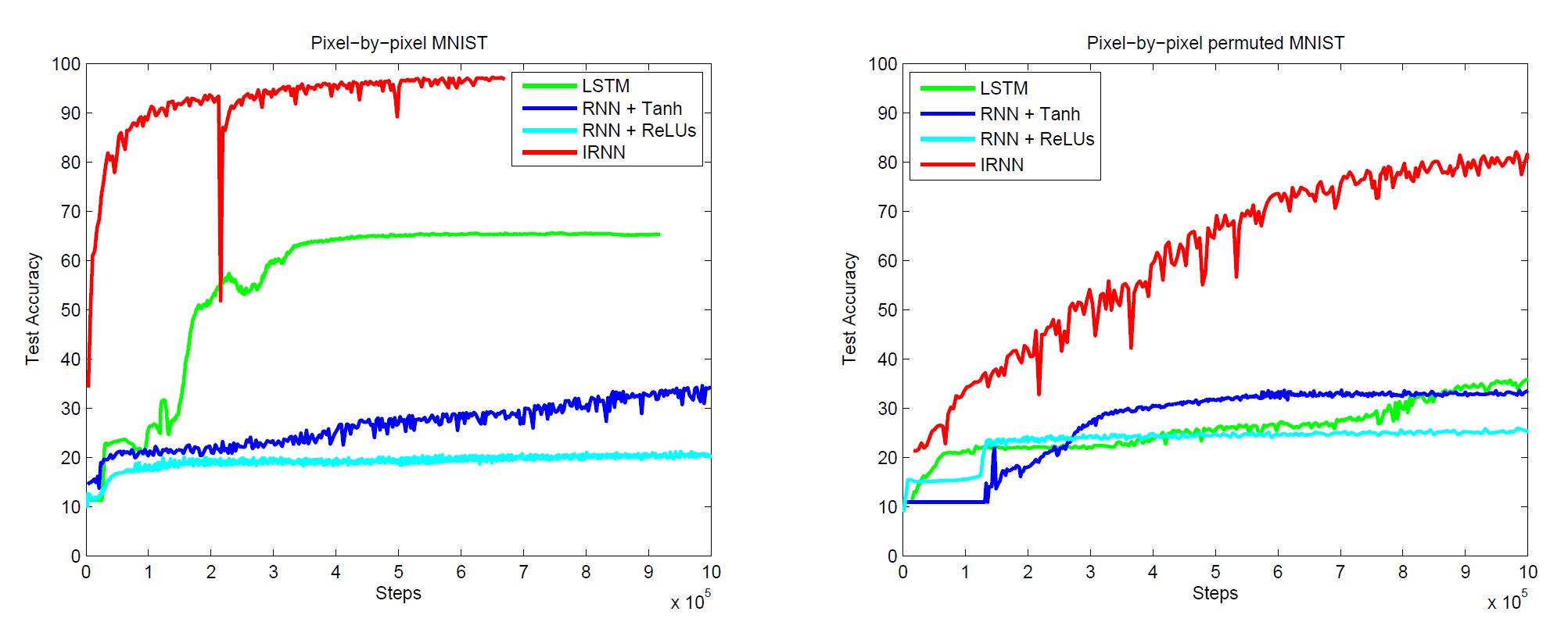
IRNN성과2

두번째 결과지는 MNIST데이터를 활용한 benchmark인데, MNIST는 pixel to pixel이기 때문에 784(28 * 28)번 time-step하기에 엄청난 장기의존성 문제가 나타날 것입니다. 해당 문제를 더 심화시키기위해, 본 연구에선 pixel을 무작위하게 permutation하도록 조정한 상태로 학습에 들어간 결과, IRNN은 LSTM보다 월등한 성능을 뽑아낼 수 있었습니다.

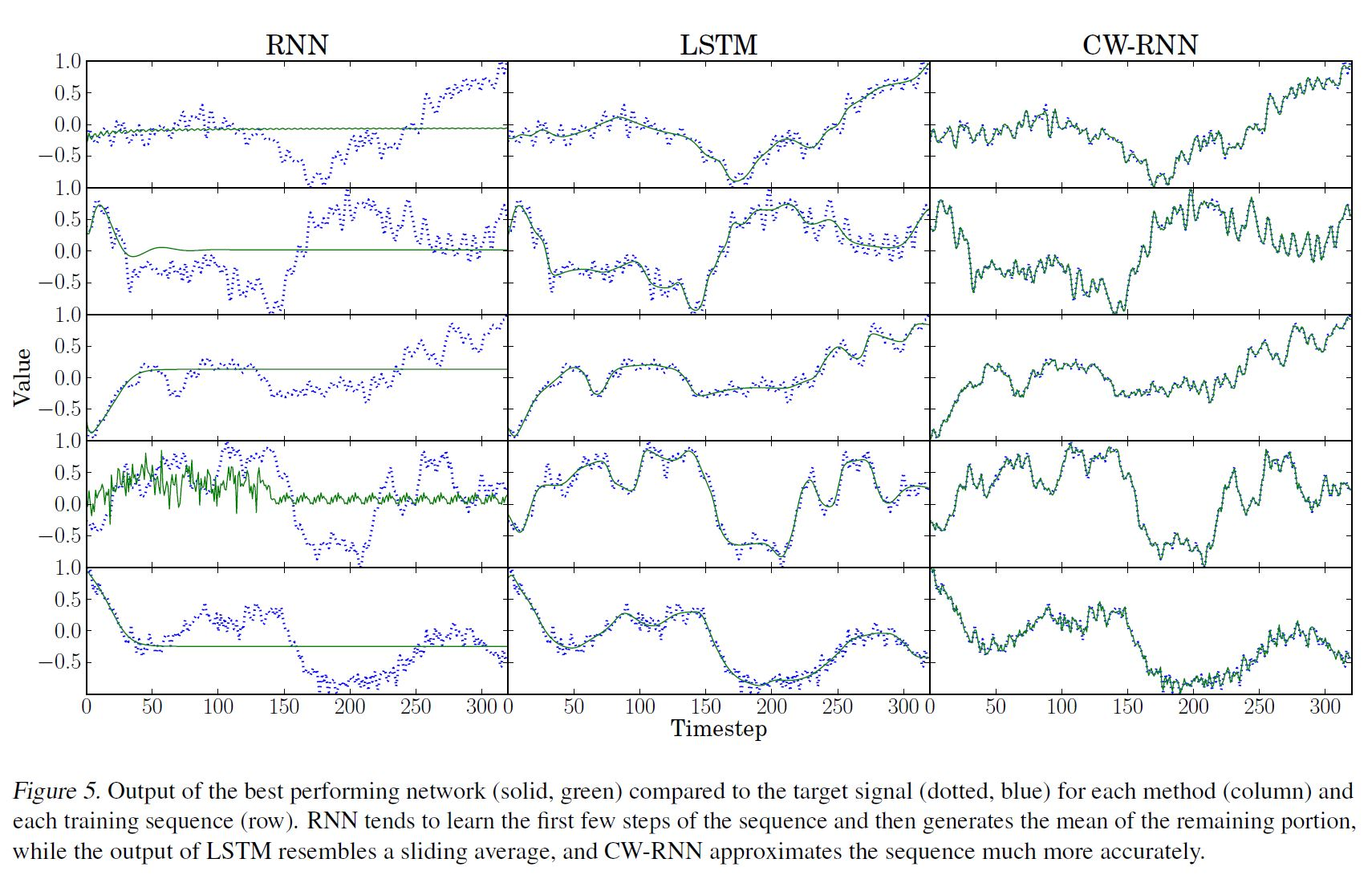
CW-RNN (clockwork RNN)

Koutn´ık, J., Greff, K., Gomez, F., and Schmidhuber, J.의 논문 『A Clockwork RNN』 에서 제안하는 CW-RNN을 통해 기존 RNN에서 발생하는 장기기억 의존성의 V&E Gradient 문제를 해결했습니다. CW-RNN의 은닉레이어를 분리된 모듈에 나눔으로써, 다른 clock speed를 적용해 작동시킨다. 이 방법으로 CW-RNN은 좀 더 효율적으로 학습할 수 있었습니다.

cw-rnn

문제점

Gradient Vanishing

시간을 많이 거슬러 올라가면(long-term) 경사를 소실하는 문제가 발생(Gradient Vanishing)

선형 함수가 아닌 비선형 함수를 Activation Function으로 쓰는 것과 비슷한 이유로, 초기값에 따라 과거데이터를 계속 곱할수록, 작아지는 문제가 발생합니다. LSTM은 구조를 개선하여 이 문제를 해결하였습니다.

Backward Flow가 안좋기에 Backpropagation을 진행할 때, Vanishing Gradient 문제가 발생. $W_{hh}$에 동일한 수를 계속해서 곱하면 두가지 문제가 발생합니다.

If 고유값(Eigenvalue) > 1 : gradient will explode
If 고유값(Eigenvalue) < 1 : gradient will vanish

예방법
1. Gradient Clipping
2. LSTM

Long-Term Dependency

이전 정보만 참고하는 것이 아니라, 그 전 정보를 고려해야 하는 경우가 있는데 시퀀스가 있는 문장에서 문장간의 간격이 커질수록, RNN은 두 정보의 맥락을 파악하기 어렵습니다. 즉, 길어진 데이터를 처리하면서 input data의 초기 time-step을 점점 잊어버리게 되는 것입니다.

Gap(time-step에 따라)이 점점 늘어날수록 RNN은 정보를 연결시켜 학습할 수 없게 됩니다. 수치로 설명해보자면 RNN은 1보다 큰 값들이 계속 발생하면 지속적으로 곱해져 발산하게 되고, 1보다 작은 값을 곱하면 0으로 수렴해 사라지게 됩니다. 이렇게 되면 RNN은 짧은 기억은 가능하지만 긴 기억은 기억하지 못하는 문제가 발생합니다.

이론적으로 RNN 모델은 파라미터값을 조정해 장기의존성 문제를 다룰 수 있으나, 안타깝게도 실전에선 전혀 그렇게 되지 못하고 있습니다.

요 약

RNN모델은 높은 유연성을 가진 모델
Vanilla RNN은 간단하긴하지만 잘 작동하지 않는다 (현업에서 사용 x), Additive Interaction이 기울기 흐름을 향상시켜주기에 보통 LSTM이나 GRU모델을 사용
RNN에서의 기울기 오차역전파는 폭발이나 손실을 일으킴